算法总结：解决Super Ugly Number问题的万用模版

2020-04-12

Ugly Number一类的问题一般是这么问的：给定k个数量的质数（k > 1），求第n个包含这些质数当中任意一个的倍数的Ugly Number。动态规划（Dynamic Programming）方法是这类问题的通用解法。

动态规划与数学归纳法

动态规划方法和离散数学的归纳法（Mathematical Induction）关系密切，而用归纳法求证需要两个条件：

当n = 1时命题成立。
假设n = m时命题成立，那么能推倒出n = m + 1时命题同样成立。

而动态规划方法无非是已知初始状态、从前一个状态推导后一个状态（或者相反），找到状态之间的状态公式是应用这种方法的关键。

动态规划的解决思路

先看看Leetcode第264题Ugly Number II：

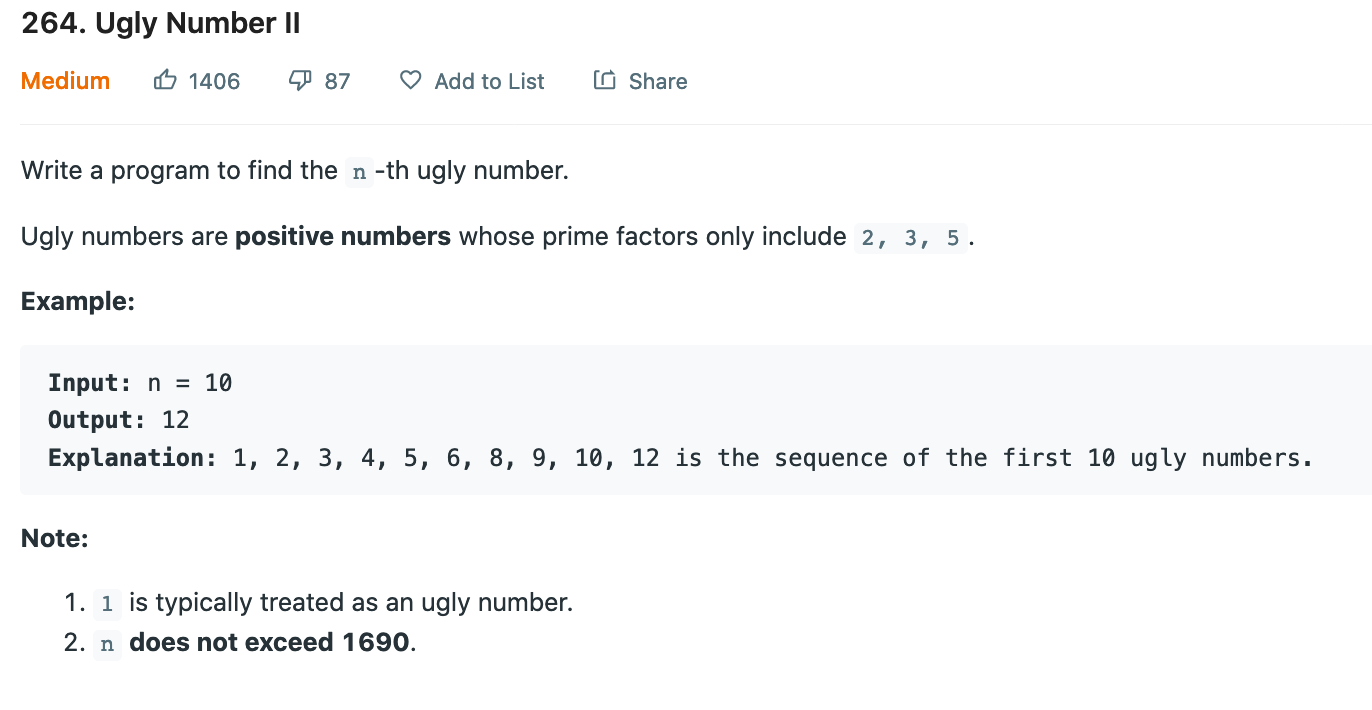
它的第四个提示如下：

Assume you have $U_{k}$ , the $k^{th}$ ugly number. Then $U_{k+1}$ must be $Min(L_{1} * 2, L_{2} * 3, L_{3} * 5)$ .

这句话是动态规划方法得以应用的重要条件，我们可以利用它推导出从当前状态到前一个状态的状态公式。

在列出状态公式之前，我们需要初始化几个数组：dp、index和primes。其中各个数组表示的是：

利用数组dp储存从小到大排列的Ugly Number。
利用数组index保存当前计算需要相乘的倍数，并规避取Ugly Number时会面临的数字重复的问题。
利用数组primes储存所有涉及到的质数。

既然已知dp[0]为1，利用计算出来的最小值求得dp[i]的值。在i达到n之前往复操作，直到求得dp[n - 1]的值。

由此可得状态公式：min = Min(primes[j] * dp[[index[j]]）。

代码实现

解决此类问题的Java代码模版，以第264题为例：

class Solution {
    public int nthUglyNumber(int n) {
        //有的题目里面函数参数就包含primes数组
        int[] primes = int[] { 2, 3, 5 };
        int[] dp = new int[n];
        //初始化index数组，使其指向dp[0]（即1），从1开始累增倍数
        int[] index = new int[primes.length];
        Arrays.fill(index, 0);
        dp[0] = 1;

        for (int i = 1; i < n; i++) {
            int min = primes[0] * dp[index[0]];

            for (int j = 1; j < primes.length; j++) {
                min = Math.min(min, primes[j] * dp[index[j]]);
            }

            dp[i] = min;

            //当min与第j + 1个质数与j + 1的积相同，则跳过这个重复
            //的数，将倍数加1
            for (int j = 0; j < primes.length; j++) {
                if (min == primes[j] * dp[index[j]]) index[j]++;
            }
        }

        return dp[n - 1];
    }
}

C++代码则如下：

class Solution {
  public:
    int nthUglyNumber(int n) {
        vector<int> primes { 2, 3, 5 };
        vector<int> dp(n, 1);
        vector<int> index(primes.size(), 0);

        for (int i = 1; i < n; i++) {
            int curr_min = primes[0] * dp[index[0]];

            for (int j = 1; j < primes.size(); ++j) {
                curr_min = min(curr_min, primes[j] * dp[index[j]]);
            }

            dp[i] = curr_min;

            for (int j = 0; j < primes.size(); ++j) {
                if (curr_min == primes[j] * dp[index[j]]) index[j]++;
            }
        }

        return dp[n - 1];
    }
}

不过对于这道题而言，由于组成的质数已定且数量很少，这个模版并不是时间空间最优的。